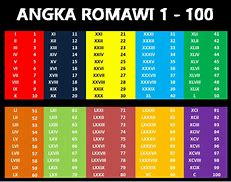
Kelas 9 Romawi

– 28 = N . Nilai N jika ditulis dalam bilangan romawi adalah .....

Correct Answer C. LXXII

ExplanationThe equation 100 - 28 = N can be simplified to 72 = N. The Roman numeral representation of 72 is LXXII.

Rumah Sinta terletak di jalan mawar nomor CXXIX .  Nomor CXXIX jika diubah ke bilangan cacah menjadi ....

Correct Answer C. 129

ExplanationThe question asks for the number CXXIX to be converted to a cardinal number. CXXIX represents 129 in Roman numerals. Therefore, the correct answer is 129.

MLV – CCCXXIV = ..... Hasil dari pengurangan di atas adalah ....

Correct Answer B. DCCXXXI

ExplanationThe given question is asking for the result of subtracting MLV (1065) from CCCXXIV (324). When subtracting Roman numerals, we need to follow the rules of Roman numeral subtraction. M (1000) cannot be subtracted from CCC (300), so we move on to the next highest value, L (50). L cannot be subtracted from CCC, so we move on to the next highest value, X (10). X can be subtracted from CCC three times, leaving us with C (100). V (5) cannot be subtracted from C, so we move on to the next highest value, IV (4). IV can be subtracted from C, leaving us with C (100) and IV (4). Therefore, the result is DCCXXXI (731).

XXI , XLI , XIX , XCI , LXI Urutan bilangan romawi di atas yang tepat dari yang terkecil adalah ....

XIX , XXI , XLI , LXI , XCI

XCI, XIX , XXI , XLI , LXI

XIX , XLI, XXI , LXI , XCI

XIX , XXI , XLI , XCI, LXI

Correct Answer A. XIX , XXI , XLI , LXI , XCI

ExplanationThe given sequence is arranged in ascending order based on the Roman numerals. Starting with XIX (19), the sequence progresses to XXI (21), then XLI (41), LXI (61), and finally XCI (91). This order represents the numbers from smallest to largest.

MM : XX + XXIII = .... Hasil dari operasi hitung campuran di atas adalah ....

Correct Answer D. CXXIII

ExplanationThe given equation is XX + XXIII. XX represents the number 20 and XXIII represents the number 23 in Roman numerals. When we add these two numbers, we get 20 + 23 = 43. In Roman numerals, 43 is represented as XLIII. Therefore, the correct answer is CXXIII.

0%0% found this document useful, Mark this document as useful

0%0% found this document not useful, Mark this document as not useful

%PDF-1.4 %Çì�¢ 5 0 obj <> stream xœlÝM¯%×yžáyÿŠJï÷sUMdâ22 dYV" ° ?ûP¤ìœ«`@‚Êlru«©[Úµ®ýüË÷×G|}þß/ÿü»Ÿ¾ýí?œïø·oÿòíó_OÌýýäìÇÞßÿõ÷ßÿû÷?{}äûáëc^ûþǬùþ¯ø6¯Ó¯ü^g>:óûOßzó|¼êû5¯¸çûŸ¾õä~¼îï{ïGÝñùäžëc÷ý—É�ûz?øú§ùÓ·úù¯÷>ÝÇžëó¯wíç_ïóÏúùç¸_çzÿsÏy}\ïXñ±ï³þü#7ûýc~þq9g}Äû�¯í�3¿ü°úúÃNþ¯®Ï_˜ëú�?ð×Ãÿô×#tíÇ5ŸgýõIÄýþ+ߟ?Ÿ8ûþ)×¹?âäÏ?ÃÿÿÏóù3ŒïøÖ�ï_Šëûç¯õ¼¦ï_ÀyÝï_ã_Ÿ¼ÏÚù>zæÇuÿû¿î×û§ñýwßþúäzÿˆüþëŸ`æýúû¯…_þåû¯¾>Þ¿,¿þÿózmþú£ý—ÿþ§ÿåÉ_ðË�ÿë¿ü~÷þ©ýË·øù÷×÷_þéw?}ÿO?|û›×Çëýïò¿{ÿn»>ÿ_?|þ"üü‡}Ï|ÿâ½Oݯ�þüëþðÓ·_þèÿûíüæûûmöÇ=¿ùýŸÿñ�ÿøÇÿýÛ¿‰ëý“Îû7?þùûßýøo?ýøç?~ÿ¯úñŸÿõÇ?üøýßÿËïÿí÷ÿüãÿùñÏ¿ýŸ?üÝ·ÿü÷¿ÿ£Î翹ïßcŸÿøóïáç³þí?ÄëË»ÏÇýþ¢®÷/Ôù<áoþøÛþ×_þÔŸÿfþú᯿Eîëúü ~^ï_Ûýå·Ùß¿ÿ‚ï¿¿ÞÎ÷ûãÎÏßh?ýåÉûï¯÷oœ+¯øù÷Ð_ž¼ÿ6Œ�é_Ÿ¼”O~ýóüéÛçß©Ÿ?Ï«>ÿÞ¹þ{õ¼¶Ÿ¿•ßðÏ?öûçÿ½ÿ®þ§¿<º¿üë=÷磞ú�«ÏÏó?<œënþÈé¾%n~øûYÿÈ×ûï˯k+øáïßl_ÿÈ|ÿ}ø~ÊøòÅŸ3jäþ,ßÿ1Ç~øUûË/åÿ÷«{½^>úúïÉûQú¨|Ô>­�Ž�.yúðôáéÃÓ‡§Ož><}xúðôáéÓÓ§§OOŸž>=}zúôôééÓÓ§§/O_ž¾<}yúòôåéËÓ—§/O_ž¾=}{úöôíéÛÓ·§oOßž¾=}{úñôü'é~þ÷yúñôãéÇÓ�§O?ž~=ýzúõôëé×Ó¯§_O¿ž~=ýzúãé�§?žþxúãé�§?žþxúãé�§¿<ýåé/OyúËÓ_žþòô—§¿<ýåéoO{úÛÓßžþöô·§¿=ýíéoOoko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ´ö¼híûÑ×ÓŸ­}?úzú÷£¯§?úzú÷£¯§?úzú÷£¯§?òô´öýÈÓÓÚ÷#OOkß�<=­}?òô´öýÈÓÓÚ÷#OOkß�<=­}?òô´öýÈÓÓÚ÷#OOkß�<=­}?òô´öýÈÓÓÚ÷#OOkß�<=­}?òô´öýÈÓÓÚ÷#OOkß�<=­}?òô´öýÈÓÓÚ÷#OOkß�<=­}?òô´öýÈÓÓÚ÷#OOkß�<=­}?òô´öýÈÓÓÚ÷#OOkß�<=­}?òô´öýÈÓÓÚ÷#OOkß�<=­}?òô´ö¼híû‘§§µŸŸ¢ûÈÓÓÚ÷#OOkß�<=­}?òô´öýÈÓÓÚ÷#OOkß�8}ØÚ°µakÃÖ†­ [¶6lmØÚ°µakÃÖ†­ [¶6lmØÚ°µakÃÖ†­ [¶6lmØÚ°µakÃÖ†­ [¶6lmØÚ°µakÃÖ†­ [¶6lmØÚ°µakÃÖ†­ [¶6lmØÚ°µakÃÖ†­ [¶6lmØÚ°µakÃÖ†­ [¶6lmØÚ°µakÃÖ†­ [¶6lmØÚ°µakÃÖ†­ [¶6lmØÚ°µakÃÖ†­ [¶6lmØÚ°µakÃÖ†­ [¶6lmØÚ°µakÃÖ¦­M[›¶6mmÚÚ´µikÓÖ¦­M[›¶6mmÚÚ´µikÓÖ¦­M[›¶6mmÚÚ´µikÓÖ¦­M[›¶6mmÚÚ´µikÓÖ¦­M[›¶6mmÚÚ´µikÓÖ¦­M[›¶6mmÚÚ´µikÓÖ¦­M[›¶Ö›/[~j]~j]~j]~j]~j]E?µ.?µ.?µ.?µ.êþ~äéýÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔºüÔº|Cܾ!nß·oˆÛ7Äíâö qû†¸}Cܾ!nß·oˆÛ7Äíâö qû†¸}Cܾ!nß·oˆÛ7Äíâö qû†¸}Cܾ!nß·oˆÛ7Äíâö qû†¸}Cܾ!nß·oˆÛ7Äíâö qû†¸}Cܾ!nß·oˆÛ7Äíâö qÛÚ¶µmkÛÖ¶­m[Û¶¶mmÛÚ¶µmkÛÖ¶­m[Û¶¶mmÛÚ¶µmkÛÖ¶­m[Û¶¶mmÛÚ¶µmkÛÖ¶­m[Û¶¶mmÛÚ¶µmkÛÖ¶­m[Û¶¶mmÛÚ¶µmkÛÖ¶­m[Û¶¶mmÛÚ¶µmkÛÖ¶­m[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µkk×Ö®­][»¶vmíÚÚµµkk×Ö®­][»¶vmíÚÚµµkk×Ö®­][»¶vmíÚÚµµkk×Ö®­][»¶vmíÚÚµµkk×Ö®­][»¶vmíÚÚµµkk×Ö®­][»¶vmíÚÚµµkk×Ö®­][»¶vmíÚÚµµkk×Ö®­][»¶vmíÚÚµµkk×Ö®­][»¶vmíÚÚµµkk×Ö®­][»¶vmíÚÚµµkk×Ö®­][»¶vmíÚÚµµkk×Ö®­][»¶vmíÚÚµµkk×Ö®­][{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖ[{lí±µÇÖúí#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xÃÖÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅ++^YñÊŠWV¼²â•¯¬xeÅûÀŠÓÖ¦­M[›¶6mmÚÚ´µikÓÖ¦­M[›¶6mmÚÚ´µikÓÖ¦­M[›¶6mmÚÚ´µikÓÖ¦­M[›¶6mmÚÚ´µikÓÖ¦­M[›¶6mmÚÚ´µikÓÖ¦­M[›¶6mmÚÚ´µikËÖ–­-[[¶¶lmÙÚ²µekËÖ–­-[[¶¶lmÙÚ²µekËÖ–­-[[¶¶lmÙÚ²µekËÖ–­-[[¶¶lmÙÚ²µekËÖ–­-[[¶¶lmÙÚ²µekËÖ–­-[[¶¶lmÙZ¿PcdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+~?òôÞÆ’�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xdÅ#+YñÈŠGV<²â‘�¬xžX±­½líek/[{ÙÚËÖ^¶ö²µ—­½líek/[{ÙÚËÖ^¶ö²µ—­½líek/[{ÙÚËÖ^¶ö²µ—­½líek/[{ÙÚËÖ^¶ö²µ—­½líek/[{ÙÚËÖ^¶ö²µ—­½líek/[{ÙÚËÖ^¶ö²µ—­½líek/[{ÙÚËÖ^¶ö²µ—­½líek/[{ÙÚËÖ^¶ö²µ—­½líek/[{ÙÚËÖ^¶ö²µ—­½líek/[{ÙÚËÖ^¶ö²µ—­½líek/[{ÙÚËÖ^¶ö²µ—­½líek/[{ÙZ¿=£5Ä­!n qkˆ[CÜâÖ·†¸5Ä­!n qkˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†øçà‘§·µâÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†x4Ä£! ñhˆGC<âÑ�†xqÙÚ²µekËÖ–­-[[¶¶lmÙÚ²µekËÖ–­-[[¶¶lmÙÚ²µekËÖ–­-[[¶¶lmÙÚ²µekËÖ–­-[[¶¶lmÙÚ²µekËÖ–­-[[¶¶lmÙÚ²µekËÖ–­-[[¶¶lmÙÚ²µekËÖ–­m[Û¶¶mmÛÚ¶µmkÛÖ¶­m[Û¶¶mmÛÚ¶µmkÛÖ¶­m[Û¶¶mmÛÚ¶µmkÛÖ¶­m[Û¶¶mmÛÚ¶µmkÛÖ¶­m[Û¶¶mmÛÚ¶µmkÛÖ¶­m[ë·g´¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܬø²µ—­½líek/[{ÙÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¶ö¶µ·­½mímko[{ÛÚ‡/Ô�·¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲâ–wXwYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲ▷¬¸eÅ-+nYqËŠ[Vܲâ~`ÅmkÛÖ¶­m[Û¶¶mmÛÚ¶µmkÛÖ¶­m[Û¶¶mmÛÚ¶µmkÛÖ¶­m[Û¶¶mmÛÚ¶µmkÛÖ¶­m[Û¶¶mmÛÚ¶µmkÛÖ¶­m[Û¶¶mmÛÚ¶µmkÛÖ¶­m[Û¶¶mmÛÚ¶µmkÛÖ¶­m[Û¶¶mmÛÚ¶µmkÛÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶ÖoÏ( qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4Ä¥!. qiˆKC\âÒ—†¸4ÄïGžÞÖÞ¶ö¶µ·­½mímko[{ÛÚÛÖÞ¾!~ù†øåâ—oˆ_¾!~ù†øåâ—oˆ_¾!~ù†øåâ—oˆ_¾!~ù†øåâ—oˆ_¾!~ù†øåâ—oˆ_¾!~ù†øåâ—oˆ_¾!~ù†øåâ—oˆ_¾!~ù†øåâ—oˆ_¾!~ù†øåâ—oˆ_ÞÆzyëåm¬—·±^ÞÆzyëåm¬—·±^ÞÆzyëåm¬—·±^ÞÆzyëåm¬—·±^ÞÆzyëåm¬—·±^ÞÆzÑÚ÷#Oïm¬—·±^ÞÆzyëåm¬—·±^ÞÆzyëåm¬—·±^ÞÆzyëåm¬—·±^ÞÆzyëåm¬—·±^ÞÆzyëåm¬—·±^ÞÆzyëåm,¿=£dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+~?òô¶VV\²â’—¬¸dÅ%+.YqÉŠKV\²â’—¬¸dÅ%+.YqÉŠKV\²âz`ÅckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µckÇÖŽ­[;¶vlíØÚ±µkk×Ö®­][»¶vmíÚÚµµkk×Ö®­][»¶vmíÚÚµµkk×Ö®­][»¶vmíÚÚµµkk×Ö®­][»¶vm­_¨‘²â”§¬8eÅ)+NYqÊŠSVœ²â”§¬8eÅ)+NYqÊŠSVœ²â”§¬8eÅ)+NYqÊŠSVœ²â”§¬8eÅ)+NYqÊŠSVœ²â”§¬8eÅ)+NYqÊŠSVœ²â”§¬8eÅ)+NYqÊŠSVœ²â”§¬8eÅ)+NYqÊŠSVœ²â”§¬8eÅ)+NYqÊŠ

Kelas 4-5 Bilangan Romawi

Bab 5 Algoritma dan Pemrograman (Dekomposisi menggunakan bahasa pemrograman C++) - Informatika SMP/MTs Kelas 9Read less

Rina lahir pada tahun 2010. 2010 jika ditulis dengan angka romawi menjadi ....

Correct Answer A. MMX

ExplanationRina lahir pada tahun 2010, yang jika ditulis dengan angka romawi adalah MMX.

Perhatikan penulisan bilangan romawi di bawah ini : I) 46 = XLVI II) 56 = LXVI III) 96 = XCVI IV) 206 = CCXV Penulisan di atas yang tepat ditunjukkan oleh nomor ....

Correct Answer D. I dan III

ExplanationThe correct answer is I dan III. This is because both I and III show the correct representation of the given numbers in Roman numerals. In I, 46 is correctly represented as XLVI, where X represents 10, L represents 50, and VI represents 6. In III, 96 is correctly represented as XCVI, where X represents 10, C represents 100, and VI represents 6.

Angka romawi V jika di belakangnya diberi angka romawi I maka bernilai ....

Correct Answer C. 4

ExplanationWhen the Roman numeral V is followed by the Roman numeral I, it represents the subtraction of I from V, which equals 4.

Angka romawi C jika di depannya diberi angka romawi X maka bernilai ....

Correct Answer B. 90

ExplanationWhen a Roman numeral X is placed in front of a larger numeral, it is subtracted from that numeral. In this case, when the Roman numeral X (which represents 10) is placed in front of C (which represents 100), it is subtracted from 100, resulting in 90. Therefore, the correct answer is 90.

MD : L = .... Hasil dari pembagian di atas adalah ....

Correct Answer C. XXX

ExplanationThe correct answer is "XXX" because the Roman numeral for 30 is represented by the letters "XXX".